

Frontline Learning Research Vol.8 No. 2 (2020) 90
- 108
ISSN 2295-3159
aUniversity of Turku, Finland
bDeggendorf Institute of Technology, Germany
Article received 27 February 2019/ revised 23 December/ accepted 26 March 2020 / available online 29 April
Interest research offers different hypotheses about the association between interest and learning outcomes. The standard hypothesis proposes that interest predicts learning outcomes: people acquire new knowledge about a topic they find interesting. The affective by-product hypothesis assumes that learning predicts interest: by learning something, people develop an interest in this topic. Finally, the reciprocal hypothesis states that interest and learning covary. This longitudinal study aimed to test the predictive validity of these three hypotheses in the context of secondary school STEM education. The participants were 104 Finnish 7th grade students aged 12-14. Data were collected at three times during the school year through questionnaires and grade evaluations in mathematics and biology. A partial least squares (PLS) path modeling approach was used to determine the relationships between interest and course grades across the three measurement points: at the beginning of the autumn semester, at the beginning of the spring semester, and after the spring semester at the end of the school year. The results differed between the autumn and spring semesters: During the autumn semester, students’ interest predicted their grades, whereas during the spring semester, grades predicted their interest. These findings indicate that the relationships between students’ individual interest towards science and mathematics with learning vary. As a practical implication, more focus should be put on when and what type of performance feedback is given to students with differing interest profiles.
Keywords: interest; learning; STEM; partial least squares (PLS) path modeling
Previous research literature has shown that students’ interest in learning science, technology, engineering, and mathematics (STEM) varies at different ages (Osborne, Simon & Collins, 2003; Hofer, 2010). The most notable change usually takes place during the transition from elementary to secondary school (Krapp & Prenzel, 2011). During that period, some students seem to start losing interest in investing effort into STEM learning while the interest of others takes a deeper and more long-lasting form. This decline in interest is particularly alarming from the perspective of how modern societies will be able to respond to a multitude of science related challenges in the future. For example, the European Commission’s report “Does the EU need more STEM graduates” (European Commission, 2015) estimates that the need for high qualification STEM jobs will generally increase throughout Europe by 2025. This is expected to coincide with a diminishing number of low qualification level jobs due to increased digitalization and robotics. Although long-term predictions of this kind are highly uncertain, it is likely that the labour market will continue shifting towards more knowledge-intensive employment and the demand for highly-skilled jobs will increase (EC, 2015). This will pose challenges for educational systems in terms of how to ensure that students will not only learn relevant skills and knowledge in schools but can also be fostered to develop a lasting interest towards science. The latter is particularly important because early interest in STEM careers has been found to predict student persistence in science and the choice of a science-related major in college (Tai, Liu, Maltese, & Fan, 2006).
Aside from encouraging adolescents to pursue careers in STEM professions, STEM education is also important from the perspective of giving students the qualifications to become scientifically literate citizens in their adult lives. This includes not only providing adequate knowledge content for different STEM topics, but also inspiring a long-lasting interest in it, as well as a basic understanding of the scientific method. To be able to do this means that the teaching provided in schools should be both cognitively satisfying, and at the same time encourage students to adopt a positive and curious mindset towards STEM.
There are several possible reasons behind the declining trends in students’ interest to learn STEM subjects. It may be that the way school education is organized, the curriculum or the quality and type of instruction do not provide enough support for students’ interest to develop further. Another explanation relates to some of the psychological demands that adolescents confront in their lives, which may cause them to view academic learning as less important compared to other aspects of life. Thirdly, it may be that students’ view of themselves as learners, their ideal self-concept, may become separated from STEM domains and hence cause them to become disinterested in investing effort in those topics (Krapp & Prenzel, 2011).
The relationship between interest and learning has been studied widely in the past research literature (Krapp & Prenzel, 2011) and recently some researchers have turned their focus on examining the directionality of the two concepts. While the prevalent view has been that interest is an antecedent for learning, some researchers have taken a different approach and aimed to determine how the acquisition of knowledge on a certain subject influences learners’ interest towards it (Rotgans & Schmidt, 2017b). If it would be so that acquiring knowledge about a school subject in fact generates and predicts students’ interest later on, then this would have consequences on how schools should design their pedagogical approaches. This would emphasize the importance of cognitive support in education and perhaps give less weight on constantly trying to come up with new and more exciting ways to get students to engage with the study topic.
The aim of this study was to contribute to this discussion by examining how the relationships between students’ interest and learning in STEM subjects develop and vary during the time period of one school year. Although the relationship between students’ interest in STEM and their academic achievement has already been studied longitudinally (i.e. Köller et al., 2001), the time points at which interest and achievement outcomes were measured have often spanned over many years. In addition, the focus of these studies has mostly been on how interest predicts students’ course choices or college majors in the STEM domain, and a more detailed view on what takes place during a single school year is needed. For this reason, the current study concentrated on revealing predictive patterns within a time frame that would be long enough to see changes but at the same time short enough to see interaction patterns.
Interest can be conceptualized as a phenomenon that arises from the interaction between a person and his or her environment (Hidi & Renninger, 2006), and which produces experimental modes that have both positive cognitive and affective qualities (Krapp & Prenzel, 2011). The cognitive qualities might include for example personally meaningful goals or viewing the activity or topic as valuable for the person’s future. Affective qualities, then, might for example relate to feeling enjoyment when interacting with the activity, or engaging deeply with the topic at hand. Theoretical literature usually acknowledges two different types of interest, namely situational and individual interest. These two types differ from each other in how much they are based on affect, knowledge and value, as well as the temporal duration of interest. Situational interest is viewed to be more affect based and temporarily fleeting, whereas individual interest is considered to connect more with the individual’s values and acquired knowledge on the subject, and be more stable over time (Krapp, Hidi & Renninger, 1992; Hidi & Renninger, 2006; Renninger & Hidi, 2011; Rotgans & Schmidt, 2017b). Both of these forms of interest can be viewed to represent different analytical levels, where situational interest refers to the actual and on-going process of engaging an activity, and individual interest the relatively stable tendency to invest time and effort in the topic of interest (Krapp & Prenzel, 2011).
Current interest theory often further divides these two different types of interest into several sub-categories which are thought to reflect their developmental phases. Krapp (2002) uses a three-category model, which divides interest into three phases of development, namely emerging situational, stabilised situational, and individual interest. Hidi and Renninger (2006) further add to this model a fourth phase by dividing individual interest into emerging and well-developed individual interest. A person’s interest is theorized to develop through each of these phases consecutively, starting from the situational interest being triggered and leading to well-developed individual interest through continued engagement with the topic, as well as increased value and knowledge acquisition (Hidi & Renninger, 2006; Renninger & Hidi, 2011).
This study concentrates on individual interest; how its emerging or well-developed phases might manifest in students’ self-reported levels of interest to study mathematics and biology during the duration of one school year. In particular, it aims to see how their interest levels reflected their grades in these subjects, and whether the grades they received predict their interest levels later on. The period of one school year was chosen as the duration of the study because it represents the natural annual cycle of students’ schoolwork, and at the same time is long enough for changes to take place in their reported interest levels or received grades, which could in turn affect their grades or reported interest levels. The context of this study was closely tied to a real-life setting in the school’s everyday life, and the aim was to acquire a general understanding of what happens to students’ interest during this one year of formal education.
Following the four-phase model by Hidi and Renninger (2011), individual interest was conceptualized as consisting of two phases, namely emerging individual interest, and well-developed individual interest. These two phases represent the last stages of interest development, when the activity, topic or domain is viewed to be personally valued, relates to the person’s existing knowledge structures, and is intrinsically motivated (Hidi & Renninger, 2006; Krapp & Prenzel, 2011). An emerging individual interest is characterized not only by positive feelings, but also by stored value and knowledge. The activity itself is of value to the person and he or she would engage it in any case if given the option to choose. This phase is usually viewed to be self-generated, although it may at times require external support from peers or experts and can, in the context of education, be affected by instructional conditions or the learning environment. This can then lead to the last phase of the model, namely well-developed individual interest which is viewed as a psychological state of interest as well as a more or less enduring tendency to engage the topic or object of interest. It has very much the same attributes as the emerging individual interest, but with more stored value and knowledge on the topic or activity. It is also viewed to be mostly self-regulated, but can benefit from instructional designs and learning environments that offer opportunities to gain knowledge through challenging tasks and interaction.
Although, the development of interest should be viewed as a continuum, separating different phases in it can have theoretical and practical value. An actually operating interest can become generated either through an already existing disposition, i.e. individual interest or through the special conditions that take place in a teaching or learning situation, i.e. the interestingness of the situation (Krapp & Prenzel, 2011). Individual interest is affected by the environmental and situational factors that take place in different learning situations. School education, with its separate lessons in different school subjects, can be viewed as a continuum in which a student’s situational interest towards the study topic may change from one time to another. A student’s experiences of focused attention and positive emotions in one learning situation may affect his or her interest in another situation later on, and gradually start to develop towards a more sustained form of interest. Meaningfulness of the task and personal involvement are seen as the pre-requisite for a person to acquire an individual interest towards a domain (Hidi & Renninger, 2006). Anchoring the phases into different intra-individual processes that take place throughout one’s interest development can for example, help teachers to adjust their teaching according to the different needs of students (Krapp & Prenzel, 2011). In this study the focus was on examining the relationships between students’ individual interest in the subjects of mathematics and biology, and their knowledge acquisition on those subjects. The aim was to examine how the predictive relationships between interest and knowledge acquisition might vary during the course of one school year. We chose to concentrate on measuring individual interest on the subject level, since this is the dominant level on which students’ learning outcomes are measured in schools. There exist also more finely grained methods to measure individual interest, for example on the sub-domain level (e.g. geometry in mathematics, or photosynthesis in biology). However, by concentrating our analyses on the level of school subjects, we aimed to provide information relevant to the work of educators and teachers, who could also benefit from the information that the results provide.
Interest has been found to have facilitating and mediating effects on learning outcomes. This has been observed in different contexts and settings, such as writing (Albin, Benton, & Khramtsova, 1996), studying psychology (Harackiewicz, Durik, Barron, Linnenbrink & Tauer, 2008), learning statistics (Hay, Callingham & Carmichael, 2015), and reading science texts (Ainley, Hidi & Berndorff, 2002). In addition, interest has been found to have a positive connection with other motivational factors such as mastery goals (Harackiewicz et al., 2008), utility value (Gegenfurtner, Knogler & Schwab, 2020), and self-efficacy (Ainley, 2012).
The traditional view in the research literature has seen interest as the prerequisite, or at least the facilitator of learning. In this study, we will call this the standard hypothesis as it is the most common way to define the relationship between interest and learning (Rotgans & Schmidt, 2017b; 2017c). The main idea behind this is that in order for learning to take place the individual has to become interested in the topic either through the support of one’s individual interest or through arousing situational factors. Individual interest can even in its less-developed form help to generate situational interest through its relation to students’ prior knowledge and value for the subject. In school education context students encounter study domains and topics that do not necessarily rank high on their list of individual interests, but they may view the information provided at the lesson as important or realize its value for completing their studies successfully. A student who is able to connect with the study content and develop strategies for working with it is more likely to start developing curiosity questions towards the topic. These curiosity questions in turn increase the student’s sense of possibilities for learning and increase the perceived value of the studied topic, which may in time become realized as more well-developed individual interest (Renninger, 2000).
Many pedagogical approaches, such as inquiry learning (Renninger et al., 2014), problem-based learning (Rotgans & Schmidt, 2011), multi-user virtual environments (Chen et al., 2015), and game-based learning (Knogler, Harackiewicz, Gegenfurtner, & Lewalter, 2015; Rodríguez‐Aflecht et al., 2018) have been developed with the aim of increasing learners’ interest towards the studied topic. All these approaches rely, at least in part, on the idea that by making the learning situation more engaging and enjoyable to the student it increases their interest, and ultimately leads to better learning outcomes. However, recent research literature has highlighted the fact that there exists incongruence between the direct effects of interest in learning, and that the empirical findings are not as self-evident as previously suggested (Köller, Baumert, & Schnabel, 2001; Nieswandt, 2007; Tapola, Veermans, & Niemivirta, 2013). Despite a significant amount of empirical research existing on interest-enhancing practices in educational settings, a considerable portion of the studies report only partial improvements or small effect sizes. This has been especially evident among sub-groups of students with differing levels of pre-existing interest (Hulleman & Harackiewicz, 2009; Renninger et al., 2014; Rodríguez‐Aflecht et al., 2018). This has caused some researchers to question whether the relationship has been viewed from the correct perspective. In their recent work, Rotgans and Schmidt (2017a; 2017b) raise the question of what would happen if the relationship between interest and learning, or knowledge acquisition, is reversed so that learning precedes interest. This proposition gains some theoretical support from the notion that individual interest may help students to remain situationally interested during learning situations, and according to the four-phase model, individual interest is more knowledge-based and less reliant on affective fluctuations (Krapp & Prenzel, 2011; Renninger, 2000). Hence it would be plausible to expect that some amount of learning has to take place before the student can start developing a longer lasting individual interest towards the study topic. In this study we call this the affective by-product hypothesis.
The third hypothesis stemming from the work of Rotgans and Schmidt (2017b) posits that interest and learning both affect each other’s development reciprocally. The lack of research on the directionality of the interest-learning relationship had already surfaced some years earlier. For example, Köller et al. (2001) already raised the question whether academic achievement necessarily follows interest, or that it could be the other way around so that those students who feel more competent in the study subject could also generate interest towards it more easily. In the reciprocal hypothesis, interest and learning are seen to interact with each other in varying degrees over time, so that their relative emphasis in the learning process differs from time to time.
In their analyses, Rotgans and Schmidt (2017b) did not find support for the so-called standard hypothesis that individual interest would precede learning. Instead they found a significant path coefficient (standardized β=0.20, p < .05) between the knowledge measured at first time point, and the interest measured at second time point; thus, supporting the affective by-product hypothesis. This means that the amount of knowledge students had at the beginning of the experiment seemed to influence their interest towards the topic at the end. Lastly, they did not find support for the reciprocal hypothesis that interest and knowledge acquisition affect each other reciprocally.
The purpose of this current study was to test these hypotheses in a classroom environment over the duration of one school year (9.5 months).
This study aimed to explore longitudinally how students’ individual interest relates to their learning outcomes in mathematics and biology during a school year. For this purpose, and based on the theoretical discussion that was presented earlier, this study addressed the following research question: What is the relationship between interest and learning in mathematics and biology education?
To examine the relationship between students’ interest and learning we formulated three theoretically derived hypotheses. These hypotheses and their relation to the theoretical model can be seen in Table 1. The partial least squares (PLS) structural equation model that was constructed to examine the relationship between the variables can be seen in Figure 1, along with the three groups of hypotheses.
Table 1
The three models and the hypotheses
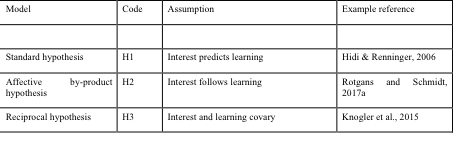

Figure 1. Hypothesized PLS model for individual interest and grades in mathematics and biology.
In the first group of hypotheses based on previous research
literature (Hidi & Renninger, 2006; Ainley, Hidi, &
Berndorf, 2002), interest was expected to predict learning. For
this, we formulated the so-called standard hypotheses. This
theoretical approach suggests that interest development precedes
learning and because of this, students’ interest at time points 1
and 2 should predict their grades at time points 2 and 3
respectively.
H1.1: Interest at time 1 predicts learning outcomes at time 2.
H1.2: Interest at time 2 predicts learning outcomes at time 3.
Second, based on the findings by Rotgans and Schmidt (2017b),
learning was expected to predict interest. For this we formulated
the so-called affective by-product hypothesis. If individual
interest would require some initial knowledge acquisition to
become generated, then the students’ grades at time point 2 should
predict their interest at the end of the school year at time 3.
H2: Learning outcomes at time 2 predict interest at time 3.
The third possible line of reasoning was based on the idea that knowledge and interest may influence each other reciprocally. In other words, interest would facilitate students’ learning, and therefore increased knowledge would in turn cause interest to increase (Rotgans & Schmidt, 2017b). To test this, we formulated the reciprocal hypothesis in which interest was expected to be reciprocally related to learning outcomes at the same time points.
Since PLS analysis does not allow testing bidirectional
relationships at the same time, we formulated two separate models
which we called primary and alternative models. These two models
differed only in terms of the direction of the simultaneous
relationship between interest and grades at time points 2 and 3.
The idea was that if interest and learning had reciprocal
relationships during the autumn semester and spring semesters,
then these relationships would manifest in the PLS analyses as
predictive connections between the two variables at simultaneous
time points 2 and 3, or be indicated by changes in these
predictive relationships during the school year.
H3: Interest and learning outcomes predict each other at one time
point or over time
The participants were 104 (53 girls, 51 boys) 7th grade students aged 12-14 from six different classes in a lower secondary school in Southern Finland. The study setting was longitudinal, following the same students through their first year of lower secondary school. Formal consent was obtained from parents for the students’ participation, and students without a letter of consent were excluded from the study as participants. Since the collection of those letters was organized by the different class teachers there is no exact number on how many students were excluded due to no consent. It can however be estimated that the number was not high, most probably less than 10%.
Data collection occurred at three time points. Time 1 was at the beginning of the autumn semester (0.5 months after starting the school year), time 2 was at the beginning of the spring semester (4.5 months), and time 3 was at the end of the spring semester (9.5 months). Students’ interest in mathematics and biology were measured on all the time points, and their learning on time points 2 and 3. In the school, teaching was divided into 5 periods each lasting about 8 weeks. Each class of students received the same amount of teaching during the school year, but the courses may have taken place in different periods. This also explains why mathematics and biology were chosen as the subjects, since they were the only two STEM subjects that the students received teaching during both autumn and spring semester.
Although there was no additional demographic data collected from the participants, it can be said that schools in Finland are generally very homogenous in terms of student population. Majority of them receive their funding through public sources, which could give support for the sample being representative. It is also not customary to collect such demographic data in Finnish schools, and in terms of the focus point of this study, these types of data were not relevant.
3.2.1 Individual interest in mathematics and biology
An instrument of Tapola et al. (2013) was used to assess students’ individual interest in mathematics and biology. To measure interest in mathematics, a single item was used (“How interested are you in mathematics”) with a five-point scale, ranging from 1 (not at all interested) to 5 (very interested). Similarly, a five-point scale single item, ranging from 1 (not at all interested) to 5 (very interested) was used to measure students’ individual interest in biology (“How interested are you in biology”) with a five-point scale, ranging from 1 (not at all interested) to 5 (very interested).
Single-item scales have previously been used to measure interest (Ainley, 2006; Palmer, 2009; Tulis & Ainley, 2011; Tapola, Jaakkola, & Niemivirta, 2014) and since we were concentrating on students’ interest in these study subjects on a generalised level, we adopted this view of measuring. The situation in which the students were asked about their interest took place outside learning situations during the school day. This arrangement reduced the possibility of students connecting the question to any particular learning situation in their everyday studies.
3.2.2 Learning outcomes
Students’ learning outcomes were measured by grade level evaluation after each semester on time points 2 and 3. Grade evaluation was done by the subject teachers and was based on students’ learning and performance throughout the whole duration of each semester. In the Finnish system students’ evaluation is based on both formative and summative assessment. The teachers observe the students’ development throughout the duration of the course and most often also use final tests to evaluate students’ learning outcomes at the end of each course. These both forms of evaluation are used to determine the course grades for each student. In this study students’ grades were used to indicate their skill and knowledge levels, and these were indicated by grades from 4 (failed) to 10 (excellent).
Correlation analysis and PLS modelling were used in the data analysis. The correlation analysis provides a more global view on relations between individual variables while the PLS modelling provides an integrated model combining all variables in one model. Descriptive statistics and correlation analyses were carried out using SPSS version 21 (IBM 2012). The structural equation models were modelled using the WarpPLS software. Partial least squares (PLS) is a structural equation modeling (SEM) technique which can simultaneously test the measurement model through relationships between indicators and their corresponding constructs, and the structural model through relationships between constructs (Gil-Garcia, 2008). PLS is efficient when working with small sample sizes and complex models, and it does not assume the data to be normally distributed (Hair, Hult, Ringle & Sarstedt, 2017). Instead of assessing overall model fit, PLS is an approach for predicting relationships in a model which were the focus in this study.
The correlation analyses presented in Table 2, show that students’ individual interest at time 1 was positively correlated with their grades at time 2 and time 3 in both mathematics and biology. In mathematics time 1 interest and time 2 grade had a moderate positive correlation (r(101) = .41, p < .01). In biology there was a moderate positive correlation between time 1 interest and time 2 grade (r(102) = .28, p < .01). These are in line with the standard hypothesis H1.1.
Table 2
Correlation of individual interest and subject grades in mathematics and biology
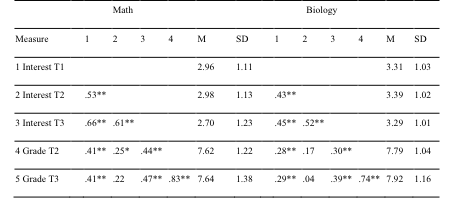
However, interest at time 2 did not correlate with grade at time 3 in either subjects, which is not in line with the standard hypothesis 1.2.
Mathematics grade at time 2 had a moderate correlation with mathematics interest at time 3 (r(91) = .44, p < .01). Similar correlation was also found in biology (r(92) = .30, p < .01). These results support the affective by-product hypothesis H2.
Regarding the reciprocity of interest and learning outcomes, interest in mathematics at time 2 was significantly correlated with mathematics grade at time 2 (r(79) = .25, p < .05) albeit the correlation being rather small. Interest at time 3 also significantly but also more sizeably correlated with mathematics grade at time 3 (r(91) = .47, p < .01. In biology correlation between interest time 2 and biology grade at time 2 was nonsignificant, but interest at time 3 and grade at time 3 had a positive correlation (r(92) = .39, p < .01). These findings only very weakly support the reciprocal hypothesis H3.
Students’ individual interest exhibited signs of stability across measurement times. In mathematics time 1 interest correlated strongly with time 2 interest (r(80) = .53, p < .01) and time 3 interest (r(92) = .66, p < .01). The relationship remained at a similar level from time 2 to time 3 (r(73) = .61, p < .01) In biology the results were similar but the effect sizes were smaller. Interest in biology at time 1 had a moderate correlations with time 2 interest (r(80) = .43, p < .01) and time 3 interest (r(92) = .45, p < .01). From time 2 to time 3 there was a strong correlation between the interest measures (r(73) = .52, p < .01). Overall these results indicate some level of stability, but also of changes.
In both mathematics and biology the grades across time were also highly correlated. In mathematics the effect size between time 2 and time 3 grades was (r(100) = .83, p < .01), and in biology (r(102) = .74, p < .01).
4.1.1 Mean level differences in students’ interests and grades between classes
Because the participants were spread to six different classes there was a possibility for the data to be nested differently in these classes. For this, intraclass correlation coefficients (ICC) were estimated for each of the measured variables for each of the six classes in order to control that their variances did not differ significantly from each other. The ICC values were estimated through variance components estimation using the type III sum of squares. Specific cut-off values for ICC that would require the use of multilevel methods usually range from 0.10 (e.g., Lee, 2000; Koo & Li, 2016) to 0.25 (e.g., Bowen & Guo, 2011). The analysis revealed excellent reliability (ICC < .10) for interest in mathematics, interest in biology, and mathematics grade at all three measurement points and for biology grade at time 2. For biology grade at time 3 the ICC estimate was 0.11. The low ICC values, and based on previous literature about the homogeneity of Finnish school classes in terms of mathematics learning (Brezovszky et al., 2019), indicated that the classes were homogenous enough, and that there was no need for multi-level methods to be used in the analyses.
The main differences between PLS modelling and more traditional methods of structural equation modelling, such as CBM-SEM or regressions based on sum-scores, are how they treat the latent variables included in the model. In CB-SEM the constructs are considered as common factors that explain the covariation between the indicators that are associated to the constructs. When estimating the model parameters in CB-SEM, the scores of these common factors are not known or needed. In PLS-SEM the constructs are represented through proxies; the weighted composites of indicator variables to that particular construct. This relaxes the assumption that all the covariation between the sets of indicators are caused by a common factor, and also facilitates accounting for measurement error, which gives it an advantage when compared with multiple regression using sum scores. Another advantage that PLS-SEM has, is its ability to produce a single specific score for each composite of each observation by establishing weights for each proxy. PLS-SEM estimates coefficients that aim to maximize the R2 values of each target variable, giving it the ability to estimate predictive patterns between the model constructs. Hence, PLS-SEM is a suitable method when the aim of the research is to develop theory and explain variance between the constructs (Hair et al., 2017)
For the PLS analysis, two sets of hypothesized path models, the primary and the alternative models were constructed for both mathematics, and biology. The models consisted of the individual interest variable (mathematics or biology) at time points 1, 2, and 3, and learning outcome variables (grades) at time points 2 and 3. The primary path models, one in each subject domain, were aimed at clarifying the standard hypotheses H1.1 and H1.2 and the affective by-product hypothesis H3. In addition, alternative models were constructed in order to complement the analyses on the behalf of the reciprocal hypothesis H3.
4.2.1 Collinearity assessment
To check for collinearity in the structural model, the average collinearity variance inflation factor (AVIF) values were obtained from the model analyses. This was done by looking at each predictor construct separately and estimating how much their variance is artificially increased by other predictor constructs in the model. An AVIF value higher than 5 exhibits a critical value (Hair et al., 2017). The AVIF values were 1.24 for the primary mathematics model, and 1.53 for the alternative mathematics model. In biology the AVIF values were 1.07 for the primary model, and 1.31 for the alternative model. These results showed that collinearity was not a critical issue in any of the structural models.
4.2.2 Coefficient of Determination
To evaluate the predictive power of a structural model, a commonly used measure is the coefficient of determination value R2. The coefficient represents the amount of variance that is explained by all of the exogenous constructs in the model that are linked to a certain endogenous construct. (Hair et al., 2017). In this study all of the exogenous constructs consisted of one-item measures, some of which also functioned as endogenous constructs. Therefore, the R2 values obtained in the analyses represent the amount of variance in a given construct explained by all of the constructs linked to it in the model. The links between constructs and the hypothesized directions of the predictive effects are indicated by arrows, and can overall be seen in Figure 1, and specified by the primary and alternative models, as well as by the mathematics and biology domains in Figures 2, 3, 4, and 5.
The average R2 value for the primary mathematics model was .37, and .37 for the alternative model. In biology these values were .28 for the primary model, and .29 for the alternative model. Among the primary models for mathematics and biology the lowest R2 value was obtained in the biology grade at time 2 construct (R2 = .09) meaning that only 9% of its variance was explained by the two constructs linked to it, namely interest in biology at time 1 and time 2. The highest value was obtained in the mathematics grade at time 3 construct where the R2 value was .69. While this construct had three explaining constructs linked to it, namely interest in mathematics at time 2 and time 3, and mathematics grade at time 2 making a higher R2 value understandable the difference is still considerable.
In the alternative models for mathematics and biology the results were very similar, with the lowest R2 value again being with biology grade at time 2 (R2 = .08), and the highest with mathematics grade at time 3 (R2 = .66).
4.2.3 Predictive relevancy of the models
Following the recommendation of Hair et al., (2017) Stone-Geisser’s Q2 values were obtained through a blindfolding procedure in order to examine the models’ predictive relevancies. In PLS path modeling, predictive relevancy means that the model also accurately predicts data that has not been used in the model estimation. In the blindfolding procedure data is re-used by deleting data points systematically and providing them a prediction of their original values, by treating them as missing values in the model. These values are then compared to the original data in order to determine the prediction error between the predicted data points and the true omitted data points. The sum of squared prediction errors is used to calculate the Q² value. Q2 values higher than 0 suggest that the endogenous construct is relevantly predicted by the model (Hair et al., 2017).
The Q2 values for mathematics variables ranged between .19 and .68 in both the primary and the alternative models, and for biology between .08 and .58 in the both models which means that all models had predictive relevancy for the constructs.
In this section the results of the Partial least squares analyses are presented. The results of the primary PLS models can be seen in Figure 2 for mathematics, and Figure 3 for biology. In addition, the results for the alternative models that aimed to complement the analyses for the reciprocal hypotheses H3, by converting the direction of the relationships between interest measures and learning outcomes at simultaneous time points, are presented in Figure 4 for mathematics, and Figure 5 for biology.
4.3.1 Standard hypotheses
Examining the first research hypotheses of whether interest predicts learning outcomes, the focus was on the primary model, which can be seen in Figures 2 and 3. Students’ interest in mathematics at time 1 predicted their mathematics grade at time 2 (β = 0.42, p < .01). In biology a similar pattern was found with time 1 interest also predicting biology grade in time 2 (β = 0.26, p < .01). However, the predictive relationship between interest at time 2 and grades at time 3 were found to be nonsignificant in both subjects. These findings supported the standard model hypothesis H1.1 but not H1.2.
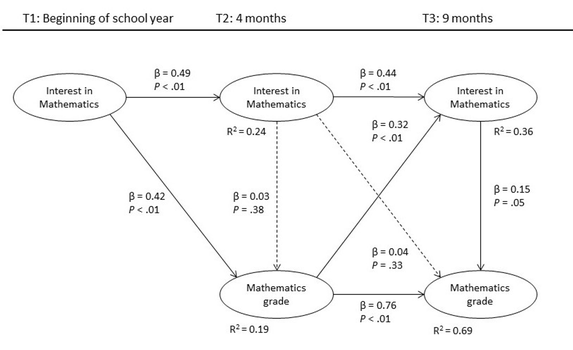
Figure 2. Primary partial least squares model of
individual interest in mathematics and mathematics grades.
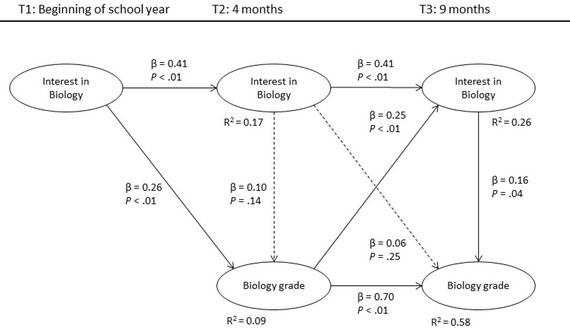
Figure 3. Primary partial least squares model of
individual interest in biology and biology grades.
4.3.2 Affective by-product hypotheses
Examining the second research question of whether learning outcomes predict interest the results were again obtained from the primary model. This choice was made because the direction of the predictive relationships concerning the affective by-product hypothesis H2 did not differ between the primary and the alternative models. Results of the analyses showed that mathematics grade at time 2 predicted interest in mathematics at the end of the school year at time 3 (β = 0.32, p < .01). Similarly, biology grade at time 2 predicted interest in biology at time 3 (β = 0.25, p < .01). These findings supported affective by-product hypothesis H2.
4.3.3 Reciprocal hypotheses
Results from the primary model analyses revealed that in both mathematics and biology, students’ interest at time 2 did not predict their grades at time 2 as the results were nonsignificant. However, there was a significant predictive effect from interest to grades at time 3 in both mathematics (β = 0.15, p < .05) and biology (β = 0.16, p < .05). Based on these results the reciprocal hypothesis H3 was supported only at time 3.
As it was already mentioned earlier, PLS analysis does not allow testing bidirectional relationships at the same time. This shortcoming was compensated by formulating an alternative model in which the direction of the relationships between interest and grades were reversed at time 2 and time 3. In the alternative model the results were similar to the standard model. In both mathematics and biology, students’ grades at time 2 did not predict their interest at time 2 as the results were nonsignificant. This meant that no support was found for hypothesis H3.1. At time point 3 students’ grades did, however, predict their interest in both mathematics (β = 0.32, p < .01) and biology (β = 0.36, p < .01) again providing partial support for the reciprocal hypothesis H3.
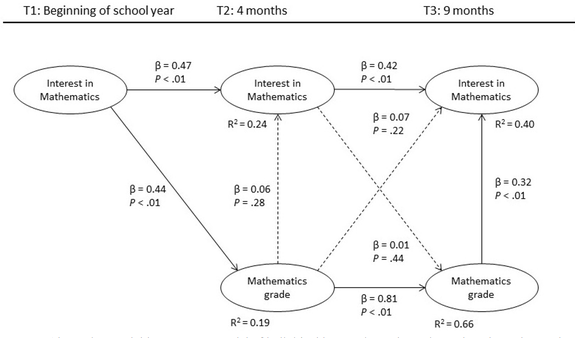
Figure 4. Alternative partial least squares model of
individual interest in mathematics and mathematics grades
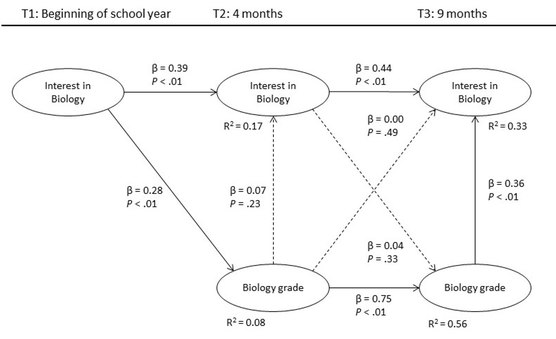
Figure 5. Alternative partial least squares model of
individual interest in biology and biology grades.
The current study examined how students’ individual interest in mathematics and biology related to their learning outcomes in these subjects. The study objective was to test the predictive validity of three different sets of hypotheses that were introduced by Rotgans and Schmidt (2017b) in the context of mathematics and biology education in secondary schools: the standard hypothesis, the affective by-product hypothesis, and the reciprocal hypothesis.
When looking at the predictive validity of the standard hypothesis, namely whether or not interest was a predictor of learning outcomes, the results differed in the autumn and spring semester. In the autumn semester students’ interest had a predictive effect on learning outcomes in both mathematics and biology. This finding was also supported by the results of the correlational analyses. When looking at the spring semester the results were quite different. In this semester, the predictive effect of interest towards learning outcomes was not found in either of the two subjects, and the correlations also became non-significant. This indicated at best partial support for the standard hypotheses that interest is an antecedent for knowledge acquisition.
In the second hypothesis, the framing was reversed, and the focus was on whether students’ learning outcomes predicted their individual interest. In this alternative model both mathematics and biology students’ grades at time 2 predicted their interest at the end of the school year. In addition, the correlation analyses revealed moderate positive correlations on both subjects across the two measurement times. In other words, students who received higher grades at the mid-semester evaluation were more likely to express higher levels of interest in the subject at the end of the school year. These results offer support for the affective by-product hypothesis.
Similar to the standard hypotheses, the results for reciprocal hypotheses of interest and learning differed between semesters. At time 2, interest did not predict learning outcomes at the same time point in either of the two subjects. Correlational analyses showed only a weak positive relationship between interest and grade in mathematics, while in biology this was not observed. However, at the end of the school year at time 3 interest did have a predictive effect on grades in both subjects and correlations were moderate. Similar pattern was also found in the alternative model where students’ grades at time 2 did not predict their interest at the same time point, but at time 3 they did. When looking over the course of the whole year however both models show a path from interest to interest through grades. This seems to indicate that the relationship between students’ interest and learning outcomes did not stay the same throughout the school year, which is in line with the reciprocity view.
To summarize, the standard hypothesis was supported only during either the autumn semester or the spring semester, but not throughout the school year. This finding was consistent across the two subjects. Thus, the affective by-product hypothesis was supported, but because it could only be tested across two measurement times between time 2 and time 3, namely spring semester, drawing too strict conclusions of these results would be premature, especially considering the fact that there were indications for reciprocity both on one time point and across time points
One explanation for these findings could relate to the differences between the measurement situations. At time 1 measurement point the students had just started their journey through secondary education and had changed to a new school with new teachers and new classmates. In this kind of environment, new external factors may have affected their interest. This aligns with the idea that in the interplay between interest and learning interest goes through an evolutional process. At first, when a student has insufficient knowledge about the topic, situational interest needs to be triggered and re-triggered before individual interest develops. Over time the effect of situational interest decreases, and more value and knowledge based individual interest becomes the decisive factor in learning (Rotgans & Schmidt, 2017c). Changes during this process (e.g. grades) may reinforce or disrupt this development.
Interest and its relation to other motivational factors as well as learning outcomes have been studied extensively in the past (e.g. Ainley et al., 2002; Hidi & Renninger, 2006; Harackiewicz et al., 2008; Krapp & Prenzel, 2011). Previous literature has often concluded that helping students become interested in the topic at hand would also help them to achieve better learning outcomes. However, evidence for interest directly predicting learning outcomes has largely been missing and this has given rise to alternative interpretations of the role interest has in the learning process. Following the ideas of Rotgans and Schmidt (2017b; 2017c) this study tested three sets of hypotheses as regards to the possible relationship that interest and learning might have during secondary school students’ school year. Based on the results we present two conclusions that should be taken into consideration in future research. Firstly, the relationship between individual interest and learning found in this study underline that this relationship is not stable throughout time, but can exhibit changes, both positive and negative, during the time period of one school year. Over longer periods of time the relationship may vary; a student might, for instance, express individual interest towards a topic or a subject but may not be able to achieve the learning outcomes he or she wished for, which may affect interest.
From the perspective of educators these findings point out the importance of designing curriculums and learning environments so that they offer experiences of success for each student. Aiming for high academic standards in schools is of course a desirable goal for education but it can also lead to some adverse effects if it is seen as the sole purpose of teaching. Receiving low grades can have a negative impact on students’ self-perceived ability and may quell their interest towards the study subject (Baumert, Schnabel & Lehrke, 1998). Supporting students’ interest in studies should in itself be viewed as an important goal since it has been found to relate to their career choices later on in life (Maltese & Harsh, 2015). Supporting students’ interest towards mathematics and science is also relevant from the perspective of 21st century skills, since societies are becoming increasingly technology-driven, and navigating in them in the future requires skills that are many times taught in STEM subjects in schools. Technology may also offer solutions for the issue of students becoming disengaged in STEM learning because of negative performance assessment. Digital learning environments can offer more individualized feedback to each learner and at the same time offer more accurate support for learning as well as learning tasks that are more finely balanced in terms of difficulty.
One theoretical contribution that this study has to offer is the longitudinal setting spanning over a whole school year that revealed patterns that are not easy to explain within the existing frameworks. Previous research literature has usually focused only on narrow time frames where hard to expect any interest development or very long time frames where development may occur, but fluctuations may also easily stay out of sight. There is no clear consensus in the research literature what would constitute an appropriate timeline for interest development. In their study, Knogler et al. (2015) carried out a science study intervention over the course of three weeks. Their findings suggest that situational interest is as its name indicates, situational, and does not transfer to other learning situations to great extent. The case with individual interest is less clear and especially the process of how and when situational interest starts to evolve into individual interest is subject to debate. Rotgans and Schmidt (2017c) criticize the four-phase model of interest development (Hidi & Renninger, 2006; Renninger & Hidi, 2011) for being too simplified and vague. Their suggestion is that situational and individual interests differ, especially in the way they are connected to knowledge. Situational interest arises from a knowledge gap that the person wants to fill, whereas individual interest can only start to develop once the person has acquired some knowledge of the object of interest. Within this view situational interest is not something that only precedes individual interest, but always exists, depends on past experiences of interest and knowledge development, and may influence further interest and knowledge development in the situation.
The findings of this study seem to indicate that mathematics and biology differ somewhat in terms of stability of interest as well as in relation to learning outcomes. In biology (M = 3.33) students rated their interest, on average, higher than in mathematics (M = 2.88) throughout the school year. This is in line with findings from previous research that biology is the more popular science subject (Baram-Tsabari, 2015) among school students. However, when looking at the correlations, the students’ interest in biology did not correlate as strongly across time points as it did in mathematics, thus indicating lower level of stability. What is perhaps even more surprising is that students’ interest in biology at the beginning of school year did not correlate with their grade either at time 2 or time 3. One explanation for this could be that biology as a subject is less clear than mathematics, causing interest in the subject to be also less stable.
The measurement used to measure individual interest in this study consisted of only one item, and although similar one-item instruments have been used in previous studies (Tapola et al., 2013; Tapola et al., 2014), it still warrants the question of how would a more fine-grained instrument have affected the results. As data for this study was collected as a part of a larger research project the choice to limit the questionnaire items was practical; keeping the questionnaire compact enough not to risk overburdening the participants. In the future, it would be recommended to widen the instrument so that it could take into consideration the value component of interest. Combining this with qualitative methods, such as interviews, would provide a better understanding of the processes that affect students’ interest development over time.
One limitation could also be that information about students’ learning outcomes were obtained only twice during the school year. Although students’ grades are the normal way of evaluating school performance, it may be that the pressure for students to receive a better final grade during the spring semester is greater than during the first half of the school year. Because their initial knowledge levels on STEM subjects were not controlled at the beginning of the school year, there was no exact way of knowing how much learning had taken place between time points 1 and 2. However, the participants were 7th graders who were on their first year of secondary education that normally lasts for three years. It can be argued that the pressure to perform well increases towards the end of 9th grade, when they need to start making choices about their future education, and the possible negative consequences of that also probably have a bigger effect.
Another limitation relates to the results of the PLS analyses. Some of the R-squared values in the model are quite low which means that the model was able to explain only a relatively small amount of the variance in some of the variables. For example, variances in students’ time 2 grades were only explained by 19% through their individual interest in both mathematics and biology. This leaves the question of what other, perhaps latent variables, would account for the rest of the variance. In addition, and perhaps more surprisingly, a large portion of variance in students’ interest at the end of the school year was left unexplained by this model. This calls for further research to investigate what other factors, external and internal, affect students’ interest development during the school year.
This research was partially supported by the Finnish Cultural Foundation.
Ainley, M. (2012) Students’ interest and engagement in classroom
activities. In S. Christenson, A. Reschly, & C. Wylie (Eds.),
Handbook of research on student engagement (pp. 283–302).
Springer. https://doi.org/10.1007/978-1-4614-2018-7_13
Ainley, M. D., Hidi, S., & Berndorff, D. (2002). Interest,
learning, and the psychological processes that mediate their
relationship . Journal of Educational Psychology, 94(3),
1–17. https://doi.org/10.1037/0022-0663.94.3.545
Albin M. L., Benton S. L., Khramtsova I. (1996). Individual
differences in interest and narrative writing. Contemporary
Educational Psychology, 21(4), 305–324.
https://doi.org/10.1006/ceps.1996.0024.
Baram-Tsabari, A. (2015). Promoting information seeking and
questioning in science. In K. A. Renninger, M. Nieswandt, & S.
Hidi (Eds.), Interest in mathematics and science learning
(pp. 135–152). American Educational Research Association.
https://doi.org/10.3102/978-0-935302-42-4
Baram-Tsabari, A., & Yarden, A. (2010) Quantifying the gender
gap in science interest.International Journal of Science and
Mathematics Education, 9(3), 523–550.
https://doi.org/10.1007/s10763-010-9194-7
Baumert, J., Schnabel, K., & Lehrke, M. (1998). Learning math
in school: Does interest really matter? In L. Hoffmann, A. Krapp,
K. A. Renninger, & J. Baumert (Eds.), Interest and
learning (pp. 327–336). Kiel: IPN.
Bong, M., Lee, S. K., & Woo, Y.-K. (2015). The roles of
interest and self-efficacy in the decision to pursue mathematics
and science. In K. A. Renninger, M. Nieswandt, & S. Hidi
(Eds.), Interest in mathematics and science learning
(pp. 33–48). American Educational Research Association.
https://doi.org/10.3102/978-0-935302-42-4
Bowen, N. K., & Guo, S. (2011). Structural equation
modeling. Oxford University Press.
https://doi.org/10.1093/acprof:oso/9780195367621.001.0001
Brezovszky, B., McMullen, J., Veermans, K., Hannula-Sormunen, M.
M., Rodríguez-Aflecht, G., Pongsakdi, N., Laakkonen E., &
Lehtinen, E. (2019). Effects of a mathematics game-based learning
environment on primary school students’ adaptive number knowledge.
Computers & Education, 128, 63–74.
https://doi.org/10.1016/j.compedu.2018.09.011
Chen, J. A., Tutwiler, M. S., Metcalf, S. J., Kamarainen, A.,
Grotzer, T., & Dede, C. (2016). A multi-user virtual
environment to support students’ self-efficacy and interest in
science: A latent growth model analysis. Learning and
Instruction, 41, 11–22.
https://doi.org/10.1016/j.learninstruc.2015.09.007
European Commission (EC)(2015). Does the EU need more STEM
graduates? Publications Office of the European Union.
https://doi.org/10.2766/000444
Gegenfurtner, A., Knogler, M., & Schwab, S. (2020). Transfer
interest: Measuring interest in training content and interest in
training transfer. Human Resource Development International,
23(2), 146–167. https://doi.org/10.1080/13678868.2019.1644002
Gil-Garcia, J. R. (2008). Using partial least squares in digital
government research. In G. D. Garson & M. Khosrow-Pour (Eds.),
Handbook of research on public information technology (Vol.
1, pp. 239–253). Information Science Reference.
https://doi.org/10.4018/978-1-59904-857-4.ch023
Hair, J. F., Hult, G. T. M., Ringle, C. M., & Sarstedt, M.
(2017). A primer on partial least squares structural equation
modeling (2nd edition.). Los Angeles: Sage.
Harackiewicz, J. M., Durik, A. M., Barron, K. E.,
Linnenbrink-Garcia, L., & Tauer, J. M. (2008). The role of
achievement goals in the development of interest: Reciprocal
relations between achievement goals, interest, and performance. Journal
of Educational Psychology, 100(1), 105–122.
https://doi.org/10.1037/0022-0663.100.1.105
Hay, I., Callingham, R., & Carmichael, C. (2015). Interest,
self-efficacy, and academic achievement in a statistics lesson. In
K. A. Renninger, M. Nieswandt, & S. Hidi (Eds.), Interest
in mathematics and science learning (pp. 203–224). American
Educational Research Association.
https://doi.org/10.3102/978-0-935302-42-4
Hidi, S., & Renninger, A. (2006). The four-phase model of
interest development. Educational Psychologist, 41(2),
111–127. https://doi.org/10.1207/s15326985ep4102_4
Hofer, M. (2010). Adolescents’ development of individual
interests: A product of multiple goal regulation? Educational
Psychologist, 45 (3), 149–166.
https://doi.org/10.1080/00461520.2010.493469
Hulleman, C. S., & Harackiewicz, J. M. (2009). Promoting
interest and performance in high school science classes. Science,
326 (5958), 1410–1412.
https://doi.org/10.1126/science.1177067
Knogler, M., Harackiewicz, J. M., Gegenfurtner, A., &
Lewalter, D. (2015). How situational is situational interest?
Investigating the longitudinal structure of situational interest.
Contemporary Educational Psychology, 43, 39–50.
https://doi.org/10.1016/j.cedpsych.2015.08.004
Koo, T., & Li, M. (2016). A guideline of selecting and
reporting intraclass correlation coefficients for reliability
research. Journal of Chiropractic Medicine, 15(2),
https://doi.org/10.1016/j.jcm.2016.02.012.
Krapp, A., Hidi, S., & Renninger, K. A. (1992). Interest,
learning and development. In K. A. Renninger, S. Hidi, & A.
Krapp (Eds.), The role of interest in learning and
development (pp. 3–25). Erlbaum.
Krapp, A., & Prenzel, M. (2011). Research on interest in
science: Theories, methods, and findings. International
Journal of Science Education, 33(1), 27–50.
https://doi.org/10.1080/09500693.2010.518645
Köller, O., Baumert, J., & Schnabel, K. (2001). Does interest
matter? The relationship between academic interest and achievement
in mathematics. Journal for Research in Mathematics Education,
32(5), 448–470. https://doi.org/10.2307/749801
Lee, V. E. (2000). Using hierarchical linear modeling to study
social contexts: The case of school effects, Educational
Psychologist, 35(2), 125–141,
https://doi.org/10.1207/s15326985ep3502_6
Maltese, A. V., & Harsh, J. A. (2015). Students’ pathways of
entry into STEM. In K. A. Renninger, M. Nieswandt, & S. Hidi
(Eds.), Interest in mathematics and science learning
(pp. 203–224). https://doi.org/10.3102/978-0-935302-42-4
Nieswandt, M. (2007). Student affect and conceptual understanding
in learning chemistry. Journal of Research in Science
Teaching, 44(7), 908–937.
https://doi.org/10.1002/tea.20169.
Osborne, J., Simon, S., & Collins, S. (2003). Attitudes
towards science: A review of the literature and its implications.
International Journal of Science Education, 25,
1049–1079. https://doi.org/10.1080/0950069032000032199
Renninger, K. A. (2000). Individual interest and its implications
for understanding intrinsic motivation. In C. Sansone & J. M.
Harackiewicz (Eds.), Intrinsic and extrinsic motivation: The
search for optimal motivation and performance (pp.
373–404). Academic Press.
https://doi.org/10.1016/B978-012619070-0/50035-0
Renninger, K. A., Austin, L., Bachrach, J. E., Chau, A., Emmerson,
M. S., King, B. R., Riley, K. R., & Stevens, S. J. (2014).
Going beyond whoa! That’s cool! Achieving science interest and
learning with the ICAN intervention. In S. Karabenick & T.
Urdan (Eds.), Motivation-based learning interventions:
Advances in motivation and achievement series (Vol. 18,
pp. 107–140). https://doi.org/10.1108/S0749-742320140000018003
Renninger, K. A., & Hidi, S. (2011). Revisiting the
conceptualization, measurement, and generation of interest. Educational
Psychologist, 46(3), 168–184.
https://doi.org/10.1080/00461520.2011.587723
Rodríguez‐Aflecht, G., Jaakkola, T., Pongsakdi, N.,
Hannula-Sormunen, M., Brezovszky, B., & Lehtinen, E. (2018).
The development of situational interest during a digital
mathematics game. Journal of Computer Assisted Learning,
34(3), 259–268. https://doi.org/10.1111/jcal.12239
Rotgans, J. I., & Schmidt, H. G. (2011). Situational interest
and academic achievement in the active-learning classroom. Learning
and Instruction, 21, 58–67.
https://doi.org/10.1016/j.learninstruc.2009.11.001
Rotgans, J. I., & Schmidt, H. G. (2017a). How individual
interest influences situational interest and how both are related
to knowledge acquisition: A microanalytical investigation. The
Journal of Educational Research,. 111(5),
530–540. https://doi.org/10.1080/00220671.2017.1310710
Rotgans, J. I. & Schmidt, H. G. (2017b). The relation between
individual interest and knowledge acquisition. British Educational
Research Journal, 43(2), 350–371.
https://doi.org/10.1002/berj.3268
Rotgans, J. I. & Schmidt, H. G. (2017c). The role of interest
in learning: knowledge acquisition at the intersection of
situational and individual interest. In P. A. O'Keefe & J. M.
Harackiewicz (Eds.) The science of interest (pp. 69–93).
Cham: Springer.
Tai, R. H., Liu, C. Q., Maltese, A. V., & Fan, X. (2006).
Planning early for careers in science. Science, 312(5777),
1143–1144. https://doi.org/10.1126/science.1128690
Tapola, A., Jaakkola, T., & Niemivirta, M. (2014). The
influence of achievement goal orientations and task concreteness
on situational interest. Journal of Experimental Education,
82(4), 455–479.
https://doi.org/10.1080/00220973.2013.813370
Tapola, A., Veermans, M., & Niemivirta, M. (2013). Predictors
and outcomes of situational interest during a science learning
task. Instructional Science, 41(6), 1047–1064.
https://doi.org/10.1007/s11251-013-9273-6
Uitto, A., Juuti, K., Lavonen, J., & Meisalo, V. (2006).
Students’ interest in biology and their out-of-school experiences.
Journal of Biological Education, 40(3), 124–129,
https://doi.org/10.1080/00219266.2006.9656029